Addition-chain Exponentiation Algorithm
It uses the fact that this exponentiation algorithm works with a pair of intermediate variables a 0a 1 storing values of the form mαmα1. An addition chain exponentiation may require an important amoun t of memory to store the intermediate powers required for the computation of subsequen t powers.
So finding an optimal addition chain amounts to finding a chain with minimal small steps.
Addition-chain exponentiation algorithm. If ai2ai-1 is called a doubling. 2r max L r holds trivally. More generally addition-chain exponentiation may also refer to exponentiation by non-minimal addition chains constructed by a variety of algorithms since a shortest addition chain is very difficult to find.
An addition-chain is used to represent the sequence which is defined as follows. At the end of the exponentiation the pair a 0a 1 equals md1md and the consistency of the computation can be verified by checking wether a 0 m equals a 1. Brauers algorithm is often called the left-to-right 2k-ary method or simply 2k-ary method.
If aiai-1 ak is called a star step. Of the modular exponentiation in advance because E is known previously. Fault Analysis is a powerful cryptanalytic technique that enables to break cryptographic implementations embedded in portable devices more efficiently than any other technique.
The largest number which has an addition chain of length r. In practice therefore shortest addition-chain exponentiation is primarily used for small fixed exponents for which a shortest chain can be precomputed and is not too large. M r med L r μ r the arithmetric average of numbers which have a shortest addition chain of length r.
For an RSA implemented with the Chinese Remainder Theorem method one faulty execution suffices to factorize the public modulus and. The variable y is multiplied h-1 times with the initial u h-2 times with the next highest powers etc. CiteSeerX - Document Details Isaac Councill Lee Giles Pradeep Teregowda.
Genetic Algorithm Modular Multiplication Cipher Text Modular Exponentiation Addition Chain These keywords were added by machine and not by the authors. A satisfying bk-. In mathematics and computer science optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications.
Chain found by the algorithm is an optimal addition chain and it does not ne ed too much space. λ ai λ ai-1 and we call this a small step. The Euclidean method was first introduced in Efficient exponentiation using precomputation and vector addition chains by PD Rooij.
M r the median of numbers which have a shortest addition chain of length r. A Brauer chain aka star-chain is an addition chain where each new element is formed as the sum of the previous element and some element possibly the same. 1 the first number is one 2 every element is the sum of two earlier elements and 3 the given number occurs at the end of the sequence.
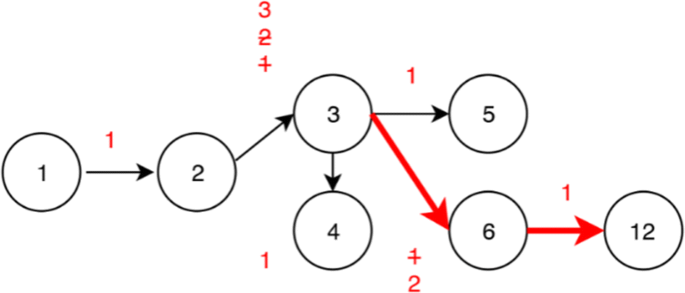
Given a natural number e an addition chain AC for e is a finite sequence of numbers having three properties. An addition-chain of length 1 for an integer n is a sequence of integers ao a1. As such it would be nice to have a list for the small powers already computed.
The shortest addition-chain algorithm requires no more multiplications than binary exponentiation and usually less. The best method for exponentiation depends strongly on the group being used the hardware the. It works by creating a shortest addition chain that generates the desired exponent.
Even given a shortest chain addition-chain exponentiation requires more memory than the binary method because it must potentially store many previous exponents from the chain simultaneously. It is extremely popular. Brauer chain is a sac for n 12509.
The algorithm uses wh-2 multiplications and w1 elements must be stored to compute x n see. If a fault is injected during the computation the coherence between a. Each exponentiation in the chain can be evaluated by multiplying two of the earlier exponentiation results.
Ask Question Asked 9 years 3 months ago. Again for step i we say that. C r min L r 2r.
This process is experimental and the keywords may be updated as the learning algorithm improves. For any given target the number of large steps is fixed by n. Where I set the initial upper limit at the number of multiplications it would take the normal binary squaremultiply algorithm and it does give the right answers but Im not satisfied with the running time it can take several seconds for numbers around 200.
The question of finding the Minimal Addition Chain MAC for needed for Addition chain exponentiation seems to be NP-complete. Addition chain-based exponentiation methods are used to find a sequence of elements in a given multiplicative group G such that the first number is 1 G and the last is s for some arbitrary s2G and 2Z.
Addition Chain Exponentiation Semantic Scholar
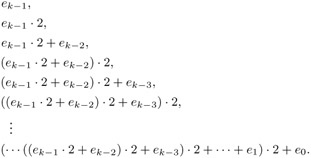6 3 Addition Chains And Windows Cryptography In C And C
Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
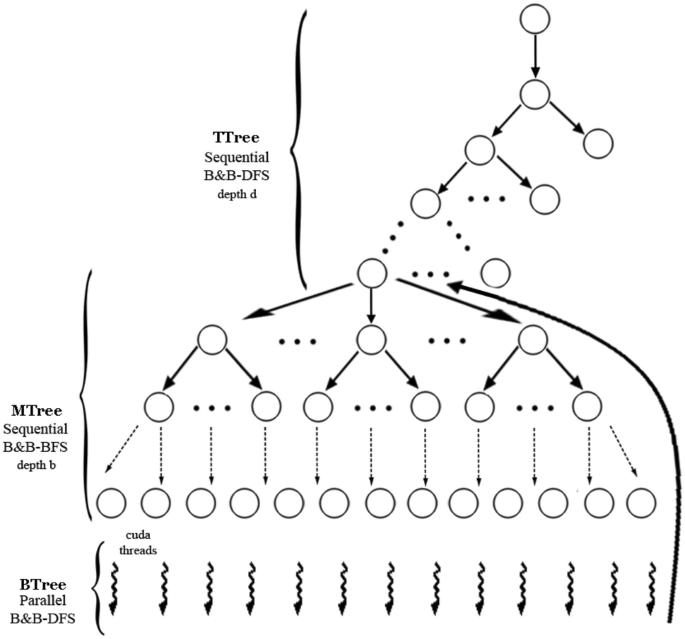A Fast Gpu Based Hybrid Algorithm For Addition Chains Springerlink
Addition Chain Exponentiation Semantic Scholar
Project Euler 122 Most Efficient Exponentiation Method Mathblog
Addition Chain Exponentiation Semantic Scholar
Evolutionary Programming For The Length Minimization Of Addition Chains Sciencedirect
A Hybrid Addition Chaining Based Light Weight Security Mechanism For Enhancing Quality Of Service In Iot Springerlink
Pdf Generation Of Addition Chain Using Deterministic Division Based Method Semantic Scholar
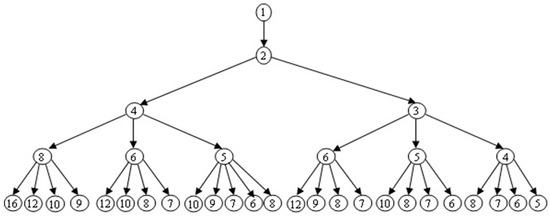Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
Addition Chain Exponentiation Semantic Scholar
Https Www Ams Org Mcom 1986 46 174 S0025 5718 1986 0829630 0 S0025 5718 1986 0829630 0 Pdf
Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
Comparison Of The Average Length Of The Addition Chains Download Scientific Diagram
